فلومتر دستگاهی است که دبی سیال را اندازه گیری می کند. فلومترها ابزارهای اندازه گیری جریان هستند که برای اندازه گیری دبی خطی، غیرخطی، جرمی یا حجمی یک گاز یا مایع استفاده می شوند. فلومتر ها به عنوان اندازه گیر جریان یا ابزار اندازه گیری جریان نیز شناخته می شوند. اندازه گیری دقیق جریان گازها و مایعات برای کنترل بهتر و کیفیت فرآیندهای صنعتی مورد نیاز است.
این مقاله به طور خلاصه اطلاعات زیر را ارائه می دهد:
- انواع فلومتر
- اصل عملکرد هر نوع فلومتر
- ویژگی های طراحی هر فلومتر
- مزایا و معایب هر نوع فلومتر
- انتخاب و کاربرد آن فلومترها
انواع فلومتر
دو نوع دبی سنج به طور گسترده در صنایع استفاده می شود:
- فلومتر حجمی
- فلومتر جرمی
فلومتر حجمی
فلومترهای حجمی نام خود را به این دلیل گرفته اند که این فلومترها حجم سیال عبوری از یک مکان خاص را در یک دوره زمانی مشخص اندازه گیری می کنند. فلومترهای حجمی یک خروجی آنالوگ، دیجیتال یا پالس آنی از نرخ جریان حجمی مایع یا گاز ارائه می کنند. انواع مختلفی از فلومترهای حجمی به شرح زیر موجود است:
- فلومتر اختلاف فشار
- صفحات اوریفیس
- متر ونتوری
- آنوبار
- وری ایبل فلومتر (روتامتر)
- فلومتر الکترومغناطیسی
- فلومتر اولتراسونیک
- فلومترهای توربینی
- فلومترهای گردابی ( ورتکس فلومتر )
- فلومتر جابجایی مثبت
فلومتر جرمی
فلومتر جرمی دبی جرمی سیالی را که در یک لوله در واحد زمان حرکت می کند اندازه گیری می کند. دو نوع فلومتر جرمی وجود دارد که در زیر به آن ها اشاره شده است:
- فلومتر جرمی کوریولیس
- فلومتر های جرمی حرارتی ( ترمال مس فلومتر )
فلومترهای اختلاف فشاری
تفاوت فشار بین طرف بالادست و پایین دست یک محدودیت در یک جریان سیال وجود دارد که رابطه مستقیم به مجذور سرعت سیال است.
Q α √ ▲P
که در آن Q = سرعت جریان حجمی و ▲P = فشار دیفرانسیل بین دو نقطه است
شکل 1 : انواع فلومتر های اختلاف فشاری
فلومتر توربین
فلومتر توربینی متشکل از یک روتور چند پره است که در زوایای قائم نسبت به جریان نصب شده و در جریان سیال روی یک یاتاقان آزاد کار معلق است، قطر روتور کمی کمتر از قطر داخلی محفظه اندازه گیری جریان است، سرعت چرخش روتور متناسب با دبی حجمی می باشد.
ویژگی های فلومترهای توربین
- فشار طراحی: 1500 PSIG
- دمای طراحی: 150 درجه سی
- اندازه: 5 میلی متر تا 600 میلی متر (نوع سوراخ کامل) / > 75 میلی متر برای نوع درج
- سیالات: مایعات/گازها و بخارات تمیز
- محدوده سرعت: 0.3 تا 15 متر بر ثانیه
- متریال: بیشتر در فولاد ضد زنگ/هستلو
- دقت: +0.25٪ تا + 0.5٪ از دبی برای نوع تمام سوراخ / + 1٪ تا + 3٪ از دبی برای نوع درج
- تکرار پذیری 10:1 است
- طول بالادست / طول مستقیم پایین دست 15/5 است
- اندازه گیری جریان دو طرفه
- برای نوع درج، هات تپ در خطوط لوله تحت فشار امکان پذیر است
مزایای استفاده از فلومتر توربین
- خیلی دقیق. معمولاً برای اثبات مترهای دیگر استفاده می شود.
- خروجی دیجیتال مجموع، دستهبندی یا ترکیب دیجیتالی مستقیم را بدون کاهش دقت فراهم میکند.
- تمایل کمتری به خواندن بالا در جریان ضربانی نسبت به کنتورهای نوع هد یا ناحیه متغیر وجود دارد.
معایب فلومترهای توربین
- در جریان های کثیف یا با مواد خورنده قابل استفاده نیست.
- در معرض رسوب گیری توسط مواد خارجی – الیاف، قطران و غیره.
- یاتاقان ها در معرض سایش یا آسیب هستند. در صورت تعویض بلبرینگ، کالیبراسیون را تغییر دهید
- ممکن است با سرعت زیاد (بیش از 150 درصد) یا شوک هیدرولیک آسیب ببیند.
- افت فشار در جریان نامی متفاوت است و می تواند زیاد باشد.
فلومتر مغناطیسی
- بر اساس قانون القای مغناطیسی فارادی عمل کنید.
- هنگامی که یک سیال رسانا در یک میدان مغناطیسی حرکت می کند، ولتاژی بین دو الکترود در زوایای قائم نسبت به سرعت سیال و جهت میدان ایجاد می شود.
- لوله جریان دارای یک منطقه و شدت میدان ثابت است، بنابراین ولتاژ توسعه یافته به طور خطی با نرخ جریان حجمی متناسب است.
شکل 4: فلومتر مغناطیسی
ویژگی های طراحی فلومترهای مغناطیسی
- فشار طراحی: 20 BARS تا 172 BARS
- دمای طراحی: تا 120 درجه سانتیگراد با آستر تفلون / 180 درجه سانتیگراد با آستر سرامیکی
- اندازه: 2.5 میلی متر تا 3000 میلی متر
- مایعات: مایعات (تمیز / خورنده / کثیف / چسبناک / دوغاب)
- محدوده سرعت: 0.1 تا 10 متر بر ثانیه
- جنس : آستر: سرامیک / تفلون / لاستیک: الکترودها: پلاتین / hastelloy / SS
- دقت: از ± 0.5٪ تا ± 1٪ جریان واقعی متغیر است.
- تکرار پذیری 10:1 است
- طول بالادست/ طول مستقیم پایین دست 5/10 است
مزایای فلومترهای مغناطیسی
- نرخ جریان تحت تأثیر چگالی سیال، قوام، ویسکوزیته، آشفتگی، یا پیکربندی لولهکشی قرار نمیگیرد.
- عدم وجود قطعات متحرک
- مقاوم در برابر خوردگی با استفاده از آستر تفلون و الکترودهای پلاتین
- محدوده اندازه گیری جریان گسترده و بدون افت فشار
معایب فلومتر مغناطیسی
- گران، نسبت به سایر انواع فلومتر.
- دمای سیالات اندازه گیری شده توسط درجه بندی مواد لاینر محدود می شود.
- نمی توان برای اندازه گیری جریان گاز استفاده کرد
فلومتر ورتکس
- یک انسداد در سراسر سوراخ لوله در زاویه قائم نسبت به جریان سیال قرار می گیرد.
- همانطور که سیال جریان می یابد، گرداب ها از طرفین متناوب خارج می شوند و این فرکانس مستقیماً با سرعت سیال متناسب است.
- تشخیص گرداب ها با استفاده از تغییرات فشار در جریان گرداب.
- نرخ ایجاد گرداب ها به طور مستقیم با سرعت جریان متناسب است.
ویژگی های طراحی ورتکس فلومتر
- فشار طراحی: 138 بار
- دمای طراحی: -200 درجه C تا 400 درجه سانتیگراد
- اندازه: 15 میلی متر تا 300 میلی متر
- مایعات: گازها (تمیز/ کثیف) و مایعات تمیز
- محدوده سرعت: 0.3 تا 10 متر بر ثانیه (مایعات) و 6 تا 80 متر بر ثانیه (گازها)
- متریال: بیشتر در فولاد ضد زنگ(استنلس استیل)، برخی از پلاستیک
- دقت: از 0.5 ± تا 1 ± درصد جریان واقعی برای مایعات و 1 ± تا 1.5 ± برای گازها متغیر است.
- تکرار پذیری 20:1 است
- طول بالادست / طول مستقیم پایین دست 5/20 است
- مزایای ورتکس فلومتر
- حداقل تعمیر و نگهداری، بدون قطعات متحرک.
- کالیبراسیون با استفاده از جریان سیال مورد نیاز نیست و تحت تأثیر ویسکوزیته، چگالی، فشار و دما در مشخصات عملیاتی قرار ندارد.
- خروجی دیجیتال یا آنالوگ
معایب فلومترهای ورتکس
- در جریان های کم، پالس ایجاد نمی شود و فلومتر می تواند کم یا حتی صفر را بخواند.
- عدد رینولدز باید بیشتر از 10000 باشد.
- لرزش می تواند باعث خطا در دقت شود.
- نصب صحیح فلومتر ورتکس بسیار مهم است زیرا یک واشر بیرون زده یا مهره های جوش می تواند باعث ایجاد گردابه شود و منجر به عدم دقت شود.
- مانند فلومترهای صفحه روزنه ای، لوله های بالادست باید طول های بلند و واضحی را فراهم کرد.
شکل 5: شکل فلومتر ورتکس، فلومتر التراسونیک و فلومتر توربین
فلومتر جرمی کوریولیس
- هنگامی که یک جرم متحرک تحت یک نوسان عمود بر جهت حرکت خود قرار می گیرد، نیروهای کوریولیس بسته به جریان جرم رخ می دهد.
- هنگامی که لوله در نیمه اول یک چرخه به سمت بالا حرکت می کند، سیالی که به داخل متر می ریزد در برابر فشار دادن لوله به پایین مقاومت می کند.
- در طرف مقابل، مایعی که از کنتور خارج میشود، در برابر کاهش حرکت عمودی آن با فشار دادن به لوله مقاومت میکند. این عمل باعث پیچ خوردن لوله می شود.
- این حرکت پیچشی توسط یک پیک آپ حس می شود و به طور مستقیم با سرعت جریان جرمی مرتبط است
ویژگی های فلومتر جرمی کوریولیس
- فشار طراحی: 345 بار
- دمای طراحی: 200 تا 426 درجه سی
- اندازه: 1.5 میلی متر تا 150 میلی متر
- سیالات/ کاربردها: مایعات (تمیز/ کثیف/ چسبناک/ دوغاب) گازهای تمیز/مایع
- محدوده جریان: 0 تا 25000 پوند در متر
- متریال : بیشتر در فولاد ضد زنگ، hastelloy / تیتانیوم
- دقت + 0.15٪ تا + 0.5٪ دبی است
- تکرار پذیری20:1 است
- اندازه گیری جریان دو طرفه
مزایای فلومترهای جرمی کوریولیس
- قادر به اندازه گیری سیالات دشوار است
- مستقل از تغییرات چگالی، مشخصات جریان و آشفتگی جریان. بنابراین نیازی به طول مستقیم نیست.
- نیازی به تعمیر و نگهداری معمولی نیست زیرا هیچ قطعه متحرکی وجود ندارد
- دقت بالا
معایب فلومترهای جرمی کوریولیس
- فلومتر کوریولس برای لوله های بزرگ در دسترس نیست (فقط تا 150 میلی متر)
- سرعت جریان بالا مورد نیاز برای تشخیص و در نتیجه افت فشار بالا
- گران بودن نسبت به سایر فلومترها
- مشکل در اندازه گیری گازهای کم فشار.
انواع صفحات اوریفیس
- صفحه سوراخ متحدالمرکز: بیشترین استفاده را دارد
- صفحه روزنه Segmental & Eccentric: برای سیالات حاوی جامدات معلق استفاده می شود.
تپینگ (Tapping ) برای صفحات اوریفیس:
- شیرهای گوشه ای (<1 اینچ)
- شیرهای D و D/2) 2 تا 16 اینچ)
- شیرهای فلنجی (> 16 اینچ)
ویژگی های صفحات اوریفیس
- فشار طراحی: بدون محدودیت. محدود شده توسط ترانسمیتر DP
- دمای طراحی: بدون محدودیت محدود شده توسط ترانسمیتر DP
- اندازه ها: حداکثر اندازه اندازه لوله است
- محدوده جریان: فقط با اندازه لوله محدود می شود.
- سیالات / کاربردها: برودتی / گازها و مایعات تمیز / بخار (اشباع / فوق گرم)
- MOC: بدون محدودیت (فولاد / مونل / نیکل / آلیاژ عجولانه)
- دقت: از 0.25 to تا 0 ± متغیر است. 5 درصد جریان واقعی دقت ترانسمیتر DP از ± 0.1٪ تا ± 0 متغیر است. 3 درصد خطا در مقیاس کامل
- بردپذیری 3:1 تا 5:1 است.
- طول بالادست / طول مستقیم پایین دست 5/20 است
مزایای اوریفیس پلیت
- به راحتی بین فلنج ها نصب می شود.
- ساخت ساده و ارزان.
- بدون محدودیت در مواد ساخت و ساز، اندازه خط و سرعت جریان
- هزینه نسبتاً مستقل از قطر لوله است زیرا هزینه DPT ثابت است.
- بدون وقفه در فرآیند برای تبادل ترانسمیتر DP.
معایب اوریفیس پلیت
- افت فشار دائمی بالا و در نتیجه مصرف انرژی بالا برای غلبه بر افت فشار.
- برای سیستم هایی با فشار استاتیکی پایین غیر عملی است.
- محدوده اندازه گیری در حدود 3:1 تا 5:1.
- دقت ها با نسبت های بتا در حدود 0.7 کاهش می یابد.
- در معرض آسیب توسط چکش آب و اجسام خارجی.
فلومتر ونتوری
یک لوله ونتوری (شکل 2) نرخ جریان را با منقبض کردن سیالات و اندازه گیری افت فشار تفاضلی اندازه گیری می کند. در مخروط بالادست فلومترونتوری ، به سرعت افزایش می یابد، فشار کاهش می یابد. افت فشار در مخروط بالادست برای اندازه گیری سرعت جریان از طریق دستگاه استفاده می شود. جزئیات بیشتر فلومتر ونتوری در اینجا ارائه شده است.
شکل. 2: نشان دهنده فلومتر ونتوری و فلومتر آنوبار
ویژگی های فلومتر ونتوری
- فشار طراحی: بدون محدودیت. محدود شده توسط ترانسمیتر DP/پرشر ریتینگ لوله.
- دمای طراحی: بدون محدودیت ، محدودیت مربوط به ترانسمیتر اختلاف فشار / و پرشر ریتینگ لوله
- اندازه: 25 میلی متر تا 3000 میلی متر
- سیالات / کاربردها: مایعات پاک / گازهای تمیز
- کاربردهای محدود: مایعات کثیف / خورنده / چسبناک و گازهای کثیف
- محدوده جریان: فقط با اندازه لوله و نسبت بتا محدود می شود.
- MOC: بدون محدودیت (چدن / فولاد کربن / SS / مونل، تیتانیوم، تفلون، هاستلوی، برنز دریایی / آلیاژ شتابزده)
- دقت: از ± 0.25٪ تا ± 0 متغیر است. 75 درصد جریان واقعی دقت ترانسمیتر DP از ± 0.1٪ تا ± 0 متغیر است. 3 درصد خطای مقیاس کامل.
- بردپذیری 3:1 تا 5:1 است.
- طول بالادست / طول مستقیم پایین دست 5/20 است
مزایای فلومتر ونتوری
- تلفات هد کمتر از صفحات روزنه ای که باعث کاهش هزینه های سرمایه ای برای پمپاژ Eqpt می شود. / صرفه جویی در هزینه های انرژی پمپ
- بدون وقفه در فرآیند تبادل ترانسمیتر DP.
- قابل استفاده برای دما بالا
- کرایوژنیک یا دماهای بالا
معایب فلومتر ونتوری
- بسیار گران است
- بزرگتر و سنگین تر است.
فلومتر آنوبار
فلومتر آنوبار دستگاهی برای اندازه گیری جریان سیال (مایع، بخار یا گاز) در یک خط لوله است. دبی با ایجاد فشار دیفرانسیل اندازه گیری می شود. طبق قضیه برنولی، این فشار دیفرانسیل متناسب با مجذور سرعت سیال در خط لوله است. فلومتر آنوبار این فشار دیفرانسیل را اندازه گیری می کند که سپس با استفاده از دستگاه ثانویه به دبی تبدیل می شود.
- پروب به عنوان سنسور فشار در خط رسانه نصب شده است.
- با جریان، پروب هر دو فشار استاتیک و دینامیکی را از طریق دهانه های پروب ثبت می کند.
- در محفظه منفی پروب ، واقع در طرف مقابل ، فقط فشار استاتیک تأثیر می گذارد
- فشار دیفرانسیل مربوط به فشار دینامیکی در خط لوله است و قوطی جریان مستقیماً محاسبه می شود.
ویژگی های فلومتر آنوبار
- فشار طراحی: تا 97 میله (38 درجه سانتی گراد) / 55 بار (370 درجه سانتی گراد)
- دمای طراحی: تا 400 درجه سانتیگراد
- اندازه: 50 میلی متر تا 3000 میلی متر
- مایعات: مایعات ، گازها و بخار را تمیز
- MOC: برنج / فولاد / فولاد ضد زنگ / Hastelloy
- دقت: از 1% تا 2±% جریان واقعی متغیر است. دقت ترانسمیتر DP از ± 0.1٪ تا ± 0 متغیر است. 3 درصد خطای مقیاس کامل.
- بردپذیری 3:1 تا 5:1 است.
- طول بالادست / طول مستقیم پایین دست 5/20 است
مزایای فلومترهای آنوبار
- سر منیفولد یکپارچه امکان نصب مستقیم ترانسمیتر های DP را می دهد
- هات تپ: ورود به خط و نصب بدون خاموش شدن سیستم
- افت فشار بسیار کم
معایب جریان سنج های آنوبار
- برای کاربردهای ویسکوز و دوغاب مناسب نیست
- فقط برای مایعات تمیز قابل استفاده است.
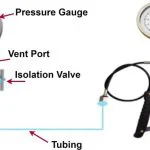
وری ایبل فلومتر ( روتامتر )
وری ایبل فلومتر یا روتامترها یکی از انواع فلومترهای رایج پرکاربرد هستند. از یک لوله شیشه ای یا پلاستیکی عمودی تشکیل شده است. اندازه لوله از بالا به پایین متفاوت است. به همین دلیل نام خود را به عنوان وری ایبل فلومتر گرفت. در داخل لوله، یک شناور اندازه گیری با حرکت آزاد وجود دارد.
- یک شناور متحرک آزاد در داخل یک لوله مخروطی عمودی متعادل می شود
- هنگامی که سیال به سمت بالا جریان می یابد، شناور زمانی که نیروهای دینامیکی وارد بر آن صفر باشد، ثابت می ماند.
- میزان جریان با موقعیت شناور نسبت به مقیاس کالیبره شده نشان داده می شود.
ویژگی های طراحی وری ایبل فلومتر ( روتامتر )
- فشار طراحی: تا 350 PSIG (لوله شیشه ای) / 720 PSIG (لوله فلزی).
- دمای طراحی: تا 400 درجه سانتی گراد (لوله شیشه ای) / 538 درجه سانتی گراد (لوله فلزی).
- اندازه: تا 75 میلی متر
- سیالات/ کاربردها: مایعات، گازها و بخارات تمیز
- محدوده جریان: حداکثر 920 مکعب در ساعت برای مایعات و 2210 مکعب در ساعت برای گازها
- MOC: شیشه بوروسیلیکات/ برنج/ فولاد/ فولاد ضد زنگ/ Hastelloy
- دقت: از 1% تا 2±% جریان واقعی متغیر است.
- بردپذیری 10:1 است
- طول بالادست/ طول مستقیم پایین دست 10/5 است
مزایای روتامترها
- خروجی ساده، قوی و خطی
- نیازی به ضربه خارجی یا خطوط سرب ندارد.
- افت فشار حداقل و نسبتاً ثابت است.
معایب روتامترها
- فقط نصب عمودی
- لوله های شیشه ای فشار و دما را محدود می کنند و در معرض شکستگی ناشی از شوک هیدرولیکی و حرارتی هستند
- لوله های شیشه ای فرسایش یافته توسط مواد جامد حل نشده و نامناسب برای اندازه گیری محلول های قلیایی
- فلومتر لوله فلزی گران تر است.
- ذرات خارجی می توانند در اطراف شناور جمع شوند و جریان را مسدود کنند
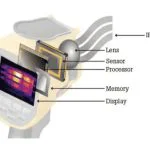
فلومتر التراسونیک
- یک جفت مبدل که هر کدام ترانسمیتر و گیرنده خاص خود را دارند، روی دیواره لوله قرار می گیرند، یکی (مجموعه) در بالادست و دیگری (مجموعه) در پایین دست.
- زمان حرکت امواج صوتی از مبدل بالادست به مبدل پایین دست (td) کوتاهتر از زمانی است که برای حرکت همان امواج از پایین دست به بالادست (tu) لازم است.
- هر چه این اختلاف بزرگتر باشد، سرعت جریان بیشتر است.
توضیحفلومتر التراسونیک را به همراه ویژگی ها، مزایا و معایب در این بخش شرح می دهیم. با ما همراه باشید…
ویژگی های طراحی فلومتر التراسونیک
- فشار طراحی: 207 بار (نوع درج) / نامحدود (بسته روی نوع)
- دمای طراحی: -180 درجه C تا 260 درجه سانتیگراد
- اندازه: 3 میلی متر تا 3000 میلی متر
- سیالات: گازهای تمیز، مایعات تمیز/خورنده (با کم/بدون جامد/حباب)
- محدوده سرعت: 0.3 تا 15 متر بر ثانیه
- متریال : بیشتر در فولاد ضد زنگ / آلیاژی
- دقت: +0.5% دبی برای نوع درج / + 1% تا 3% دبی برای گیره روی نوع
- تکرار پذیری 10:1 تا 300:1 است
- طول بالادست/ طول مستقیم پایین دست 10/5 است
- اندازه گیری جریان دو طرفه
- برای نوع درج، هات تپ در خطوط لوله تحت فشار امکان پذیر است
مزایای فلومتر التراسونیک
- بدون مانع / قطعات متحرک در مسیر جریان
- بدون افت فشار
- هزینه نگهداری کم
- مدل های چند مسیره دقت بالاتری برای محدوده وسیع تری از عدد رینولدز دارند
- می تواند در جریان سیال خورنده استفاده شود
- مدل های قابل حمل برای تجزیه و تحلیل میدانی و تشخیص موجود است
معایب فلومتر های اولتراسونیک
- فقط مایعات و گازهای تمیز را می توان اندازه گیری کرد
- هزینه راه اندازی اولیه بالاتر
فلومترهای جابجایی مثبت
- این متر به طور مکرر مایع را در یک مقدار مشخص به دام می اندازد و سپس آن را خارج می کند.
- مقدار مایعی که عبور کرده است بر اساس تعداد گیر افتاده است.
- دبی حجمی را می توان از روی سرعت چرخش دستگاه مکانیکی محاسبه کرد.
ویژگی های فلومترهای جابجایی مثبت (PD).
- فشار طراحی: 1500 PSIG (مایع)/: 100 psig (گاز)
- دمای طراحی: 293 درجه C (مایعات)/: -34 تا 60 درجه. C (گازها)
- اندازه: 6 میلی متر تا 400 میلی متر
- سیالات: مایعات / گازهای تمیز
- محدوده جریان: 0 – 20000 GPM (مایعات)/: 0 – 3000 مکعب در ساعت (گاز)
- متریال : بیشتر در آلومینیوم، فولاد ضد زنگ، پلاستیک، hastelloy
- دقت + 0.5٪ تا + 1٪ دبی است
- تکرار پذیری 15:1 است
شکل 6 : فلومترهای جابجایی مثبت و فلومترهای جرمی حرارتی
مزایای فلومترهای PD
- دقت خوب و تکرار پذیریبالا
- می تواند در جریان مایع چسبناک استفاده شود
- هزینه راه اندازی اولیه کم تا متوسط
- بدون نیاز به منبع تغذیه و در طیف گسترده ای از دستگاه های خواندنی موجود است
معایب فلومترهای PD
- به دلیل «قطعات متحرک» نیاز به تعمیر و نگهداری در فواصل زمانی مکرر است.
- افت فشار بالا به دلیل انسداد
- برای دبی کم مناسب نیست
- برای سیالات با مواد جامد معلق مناسب نیست
- گاز (حباب) در مایع می تواند به طور قابل توجهی دقت را کاهش دهد
فلومتر جرمی حرارتی
- با نظارت بر اثر خنک کننده جریان گاز هنگام عبور از روی مبدل گرم شده عمل می کند.
- جریان گاز از روی دو مبدل PT100 RTD عبور می کند.
- مبدل دما دمای واقعی فرآیند گاز را کنترل می کند، در حالی که مبدل خود گرم شده با تغییر جریان عبوری در دمای دیفرانسیل ثابت نگه داشته می شود.
- هر چه جریان جرمی که از روی مبدل گرم شده عبور می کند بیشتر باشد، جریان مورد نیاز برای ثابت نگه داشتن دمای دیفرانسیل بیشتر است.
بنابراین، جریان بخاری اندازهگیری شده، معیاری از نرخ جریان جرمی گاز است.
ویژگی های طراحی فلومترهای جرمی حرارتی
- فشار طراحی: 1200 PSIG
- دمای طراحی: 176 درجه سانتی گراد
- اندازه: 15 میلی متر تا 1000 میلی متر
- سیالات: گازهای تمیز
- محدوده جریان: 0 – 2500 SCFM
- متریال: بیشتر در فولاد ضد زنگ / شیشه، تفلون، مونل
- دقت 1% تا +2% دبی است
- تکرار پذیری 10:1 تا 100:1 است
- طول بالادست / طول مستقیم پایین دست 5/3 است
مزایای فلومتر جرمی حرارتی
- نیازی به جبران دما یا فشار نیست
- خروجی خطی (از آنجایی که اختلاف دما متناسب با جریان جرم است)
- در صورتی که مواد مناسب مشخص شده باشد، می تواند بر روی جریان های فرآیند خورنده استفاده شود
- ولتاژ DC یا خروجی های 4 تا 20 میلی آمپر dc موجود است
معایب فلومترهای جرمی حرارتی
- فقط برای جریان گاز عملی است
- در معرض انسداد توسط ذرات خارجی یا رسوبات رسوب شده به دلیل منافذ کوچک در فلومتر
- نیازهای برق بیش از حد در اندازه لوله های بزرگتر
- برای سرویس دهی باید از خط فرآیند خارج شود
- کالیبراسیون میدان دقیق دشوار است
کاربرد فلومترها / انتخاب فلومتر
مایعات/گازهای تمیز
مناسب ترین فلومتر کدام است؟
اوریفیس ها
ونتوری
آنوبار
وری ایبل فلومتر
مغناطیسی (فقط مایعات)
اولتراسونیک
ورتکس
فلومترهای جرمی کوریولیس
فلومتر جرم حرارتی (فقط گازها)
PD متر
مایعات کثیف
مناسب ترین فلومتر کدام است؟ فلومتر مغناطیسی/کوریولیس
کاربردهای محدود: فلومتر وتنوری
گازهای کثیف
مناسب ترین: ورتکس فلومتر
کاربردهای محدود: فلومتر ونتوری/ فلومتر جرم حرارتی / وری ایبل فلومتر
مایعات خورنده: جریان سنج مغناطیسی / جریان سنج التراسونیک
مایعات غیر نیوتنی: جریان سنج جرمی کوریولیس
مایعات چسبناک: کوریولیس / مغناطیسی / جابجایی سنج مثبت
دوغاب های ساینده: فلومترهای مغناطیسی/جریان سنج جرمی کوریولیس
دوغاب های فیبروسی: فلومترهای مغناطیسی/جریان سنج جرمی کوریولیس (کاربردهای محدود)
بخار اشباع شده
مناسب ترین: دبی سنج های Orifice DP/Vortex
کاربردهای محدود: متر ونتوری / متر مساحت متغیر
بخار فوق العاده گرم
مناسب ترین: Orifice DP متر
کاربردهای محدود: متر ونتوری
کاربردهای برودتی: ونتوری متر/صفحات اوریفیس
پارامترهای موثر بر انتخاب فلومتر
عوامل مختلفی بر انتخاب فلومتر برای یک فرآیند صنعتی خاص تأثیر می گذارد. برخی از آن عوامل عبارتند از:
- فاز سیال؛ به عنوان مثال: گاز، مایع، بخار
- شرایط جریان و محدوده جریان؛ به عنوان مثال: مایع تمیز، کثیف، ساینده یا چسبناک.
- پارامترهای طراحی فرآیند؛ به عنوان مثال، فشار، محدوده دما، چگالی.
- اندازه لوله
- دقت مورد نظر
- مواد ساخت و ساز (سیال خورنده یا غیر خورنده).
- تکرارپذیری و مقرون به صرفه بودن
- ملاحظات زیست محیطی، در صورت وجود.
نصب فلومتر
اندازه گیری جریان با استفاده از فلومترها یک فعالیت ضروری برای هر صنعتی است. بنابراین، باید داده های قابل اعتماد و دقیق ارائه دهد. دقت و تکرارپذیری داده های اندازه گیری شده تا حد زیادی به نصب صحیح فلومتر بستگی دارد. برخی از مراحل حیاتی که باید در هنگام نصب فلومتر دنبال شود در زیر ذکر شده است:
– باید در محل مناسب نصب شود.
– در جاهایی که ارتعاش یا میدان مغناطیسی وجود دارد نباید نصب شود.
– جهت جریان باید قبل از نصب مشخص باشد.
– فلومترها باید روی لوله مستقیم نصب شوند.
– برخی از فلومترها ممکن است به طول مستقیم در بالادست و پایین دست فلومتر نیاز داشته باشند. برای نتایج دقیق باید حفظ شود.
– برای کاربردهای جریان مایع، جریان رو به پایین باید اجتناب شود.
– اطمینان حاصل کنید که فلومتر کاملاً با مایع پر شده است.
– از بخار یا هوا در خطوط مایع و قطرات مایع در خطوط گاز باید اجتناب شود.
– نصب فیلتر در بالادست فلومتر برای حذف مواد جامد ترجیح داده می شود.
– در صورت نیاز به تعمیر، یک خط عبور باید ارائه شود.